ФОРМУВАННЯ В МАЙБУТНІХ УЧИТЕЛІВ ТВОРЧОГО ПІДХОДУ ДО ПІДГОТОВКИ УРОКУ МАТЕМАТИКИ

Аліна Воєвода
(Вінниця, Україна)

В статті розглянутоможливості застосування активних методів та прийомів навчанняв процесі вивчення курсу «Основ педагогічної майстерності» з метою формування в майбутніх учителів математики індивідуального стилю педагогічної діяльності, творчого підходу до підготовки та проведення нестандартних уроків математики. Наведено теми уроків-вистав з математики для основної й старшої школи, вимоги до їх організації й проведення, фрагменти уроків-вистав з математики.

Ключові слова: педагогічна майстерність, творчий підхід,  урок-вистава.

В статье рассмотрены возможности применения активных методов и приемов обучения математики в процессе изучения курса «Основ педагогического мастерства» с целью формирования у будущих учителей математики индивидуального стиля педагогической деятельности, творческого подхода к подготовке и проведению нестандартных уроков. Приведены темы уроков-спектаклей по математике для основной и старшей школы, требования к их организации и проведению, фрагменты уроков-спектаклей по математике.

Ключевые слова: педагогическое мастерство, творческий подход, урок-спектакль.

The article discusses the possibilities of using active methods and techniques in the course of studying«Fundamentals of Pedagogical Skills» in order to help future teachers of Mathematics to form individual style of pedagogical activity, creative approach to the preparation and carrying of non-standard lessons. The articles presents the topics of the lesson-spectacles on Mathematics for secondary schools, the requirements for their organization and conduction, a sample script of lesson-spectacle on Mathematics.

Keywords: pedagogical techniques, creative approach, lesson-spectacle.

Постановка проблеми. Одним із найважливіших стратегічних завдань модернізації системи вищої освіти України є забезпечення якості підготовкифахівців на рівні міжнародних вимог, виховання самостійності, відповідальності, формування їхньої активної життєвої позиції.

В контексті компетентнісного підходу визначальними й ефективними для успішної професійної діяльності є не стільки розрізнені знання, скільки узагальнені вміння та навички, які проявляються в здатності вирішувати професійні проблеми, у володінні інформаційними технологіями, здатності до спілкування.

Головним завданням учителя математики є нині «виховання особистості, формування її мотиваційної сфери, моральних цінностей і переконань. Формування знань, умінь і навичок з математики є складовою частиною цього виховання і тим процесом, у якому це виховання здійснюється» [8: 61]. Тому важливо ще в процесі підготовки майбутнього вчителя математики формувати його не лише як компетентного фахівця-математика, а й як особистість із високою педагогічною і загальною культурою, здатну проявляти творчий підхід до виконання професійної діяльності.

Аналіз попередніх публікацій. Аналіз педагогічної літератури свідчить, що в наукових пошуках вітчизняні та закордонні вчені в різних аспектах звертались до проблематики професійної підготовки вчителя (В. Андрущенко, С. Гончаренко, Р. Гуревич, В. Кремень, Н. Кузьміна, Ю. Кулюткін, А. Маркова, М. Никандров, І. Підласий, Б. Скіннер, В. Сластьонін,  Н. Хмель та ін.).

Проблемам професійної підготовки вчителя математики присвячені роботи І. Акуленко, Г. Бевза, В. Бевз, М. Бурди, М. Віленкіна, В. Гусєва, О. Дубинчук, О. Матяш, В. Монахова, О. Мордковича, В. Моторіної, В. Орлова, О. Скафи, З. Слєпкань, Н. Стефанової, А. Столяра, Н. Тарасенкової, І. Тесленка, В. Швеця.

В останні десятиліття проблему педагогічної майстерності розробляли Е. Барбіна, І. Зязюн, Л. Кандибович, О. Пєхота, С. Сисоєва, В. Сластьонін, В. Сухомлинський, А. Щербаков та ін. В їхніх працях розглядаються питання підготовки творчого вчителя, викладача, з яскравою індивідуальністю, здатного до безперервного самовиховання і самоосвіти. Отже, проблема творчого становлення майбутнього вчителя і в наш час привертає увагу науковців.

Мета статті  – розглянути можливості формування в майбутніх учителів творчого підходу до підготовки уроку математики в процесі вивчення курсу «Основ педагогічної майстерності».

Виклад основного матеріалу.  «Професійна діяльність учителя математики – це, насамперед, педагогічна діяльність, пов’язана з розвитком учнів у процесі навчання математики» [5: 126].  Особливість такої діяльності в тому, що її цілі й завдання не даються остаточно в готовому вигляді. Постійно розв’язуючи типові і нестандартні педагогічні задачі, вчитель, як і будь-який інший дослідник, будує свою діяльність відповідно до визначених загальних етапів розгортання евристичного пошуку: а) аналіз педагогічної ситуації; б) проектування результату відповідно до початкових даних; в) аналіз наявних засобів, необхідних для перевірки припущення та досягнення необхідного результату; г) оцінка отриманих даних; д) формулювання нових завдань [7]. При цьому творчості відводиться важлива роль там, де педагогічна наука та багаторічний досвід не дають чіткої відповіді на питання як діяти.

Вітчизняний вчений І. Зязюн вважає творчий підхід до розв’язання проблем навчання провідною якістю фахівця та одним із важливих компонентів педагогічної майстерності. Проте часто студенти не готові проявляти творчий підхід до підготовки уроку математики, внаслідок чого не можуть чітко передбачати динаміку навчально-виховного процесу, проектувати й прогнозувати розвиток особистості студента з урахуванням його здібностей і особливостей.

Саме на заняттях з «Основ педагогічної майстерності» (для студентів напряму підготовки «Математика*») з’являється можливість приділити увагу питанням формування творчого підходу до підготовки уроку математики.

Під час вивчення змістового модуля «Формування індивідуального стилю педагогічної діяльності вчителя математики» студенти можуть різнобічно і критично оцінювати різні методи, прийоми, засоби навчання математики. Для цього ми пропонуємо їм не лише проектувати, але й проводити нестандартні уроки, які мають «нетрадиційну (невстановлену) структуру») [6: 232]. На таких уроках педагог «організовує творчу діяльність учнів, які самостійно «створюють» новий для себе продукт: нові знання, нову систему дій, новий метод досягнення тощо» [4: 54-55]. Крім навчально-пізнавальної діяльності, на нестандартному уроці задіяні різні види діяльності (ігрова, творча, змагальна, пошукова) та активні методи і прийоми навчання (імітаційні рольові ігри, інтерактивні технології навчання, театральні дійства тощо), завдяки яким можна підвищити ціннісне ставлення учнів до навчального  матеріалу.

Для проведення лабораторного заняття з теми «Творчий підхід до режисури уроку математики» у вигляді імітаційної рольової гри ми пропонуємо студентам об’єднатися в малі групи (5-7 чоловік) та обрати, наприклад, тему уроку-вистави самостійно, або з поданого викладачем списку («Що вивчає математика?» (5 клас), «Ознаки подільності» (6 клас), «Трикутник» (геометрія, 7 клас), «Теорема Піфагора» (геометрія, 8 клас), «Арифметична та геометрична прогресії» (алгебра, 9 клас), «Побудова перерізів» (геометрія, 10 клас ), інтегрований урок-вистава «Первісна та інтеграл» (алгебра і фізика, 11 клас)). При цьому наголошуємо студентам, що вистава на уроці математики має не лише зацікавити учнів предметом, формувати їх пізнавальні та мотиваційні інтереси, виробляти позитивні якості характеру особистості (працьовитості, наполегливості у досягненні мети тощо), але й розвивати образне мислення, творчий потенціал та здібності учнів.

Викладач забезпечує педагогічну підтримку при підготовці малих груп до обраного уроку-вистави, створює на занятті сприятливі психологічні умови для педагогічної взаємодії та спілкування.  Наприкінці заняття викладач підводить підсумки, акцентує увагу студентів на важливих аспектах теми [5: 240-242].

Наведемо фрагмент уроку-вистави «Ознаки подільності» (6 клас).

Мета уроку: узагальнити і систематизувати знання учнів про прості і складені числа, ознаки подільності; розвивати інтерес до математики; вчити учнів культурі спілкування.

«Вчитель. Друзі, ви вже знаєте, що натуральні числа поділяються на прості і складені. То ж які числа називаються простими? Наведіть приклад.

–А які числа називаються складеними?

– Яке число вважають ні простим, ні складеним? (Відповідь учнів – одиниця ).

З’являться цифри.

Одиниця. І нехай так, але все одно всі цілі числа з одиниць складаються. А говорячи про прості числа, одиницю обов’язково згадують.

Входять Евклід, Ератосфен, Я. П. Кулик.

Евклід. Для мене прості числа теж добре знайомі.

Одиниця. А ви хто?

Евклід. Я – Евклід. В перекладі з давньогрецької моє ім’я означає «добра слава». Більше 2300 років тому я довів, що за кожним простим числом слідує більше просте число, тобто найбільшого простого числа не існує.

Ератосфен (в руках з дощечка, в якій просвердлені дірочки). А я в праці «Решето» (ІІІ ст. до н. е.) виклав метод знаходження простих чисел, які не перевищують даного натурального числа. На дощечці, вкритій воском, я послідовно проколював у воску дірочки над числами, кратними 2, 3, 4,…, внаслідок цього дощечка стала схожою на решето, крізь яке ніби просіювали складені числа, а залишались прості. Так я склав таблицю простих чисел до 1000. А мій спосіб знаходження простих чисел назвали решетом Ератосфена. 

Кулик. Мої «математичні таблиці для учнів є тим, чим є залізничі колії для подорожуючих, оскільки переносять їх дорогою майже чарівною через усі перешкоди та негаразди, що наближаються, а також пояснюють труднощі, які у вивченні математики як правило знаходять».

Одиниця. Пробачте.  Пане… ?

Кулик. Яків Пилип Кулик – професор математики Празького університету. Я народився у Львові у 1793 році. Після закінчення гімназії вивчав філософію в Львівському університеті. Останніх 20 років життя я присвятив складанню таблиць простих чисел, викладених у праці «Великий канон дільників всіх чисел, що не діляться на 2, 3 і 5 та простих чисел, що містяться між ними до 100 330 201», яка складалась з 4212 сторінок.

Нуль. Ці не надруковані і донині таблиці більш як через 100 років після перевірки використали нідерландські математики при складанні таблиці простих чисел для одинадцятого мільйона, виданої в 1951 році  в Амстердамі. 

Двійка (ліниво). Досить вже про прості числа говорити. У них всього два дільники: 1 і саме число. До того, крім мене, вони всі непарні. А от ознака подільності на 2 всім знайома. Правда ж? (Відповідь учнів).

Двійка. Отже, головне, щоб число закінчувалось парною цифрою. Тебе, Нулику, до них теж відносять.  

П’ятірка. А чого  ти лише про ознаку подільності на 2 говориш? Хіба моя ознака менш потрібна? Друзі, ви ж знаєте ознаку подільності на 5? (Відповідь).

Трійка. Але без знання ознак подільності на 3 і на 9 теж не обійдешся.

Дев’ятка. Підніміть руку, хто їх знає. Нам буде дуже приємно почути добрі слова про себе. (учні формулюють ознаки, наводять приклади).

Сімка. А от дізнатися чи ділиться число на 11 набагато складніше. 

Трійка. Ти б краще помовчала. Можна подумати, що ознака ділення на 7...

Сімка. Моя ознака формулюється складно. Але можна дати опис її перевірки. Відділимо від числа дві останні цифри. Додамо відділене число з подвоєним числом зліва. Якщо сума ділиться на 7, то і число ділиться на 7. А можна інакше. Відділити три останні цифри. Число на дві частини розділиться. Знайдемо їх різницю. І так будемо робити до тих пір, поки не одержимо число менше 1000. А тоді вже перевіримо діленням (Слайд з прикладом).

Шістка. Такий спосіб підходить і для ознак подільності на 11 і на 13…

Четвірка. Схожим способом можна перевірити чи ділиться число на 37. Розіб’ємо число справа наліво на групи по три цифри ( в самій лівій може бути і менше цифр) і додамо всі групи. Якщо вийде число більше тисячі, повторимо розбиття. Коли отримаємо тризначне число розділимо на 37(Слайд).

Одиниця. От бачите, з подільністю чисел не все так просто.

З’являється Факір. Я доведу, що знання ознак подільності допомагає стати ясновидцем. В мене в руках книга. Я зможу назвати перше слово на сторінці, вказаній вами. Запрошую когось з вас допомогти мені. Запишіть будь-яке двоцифрове число. Припишіть справа і зліва це саме число. Поділіть це шестизначне число на 3, одержаний результат на 7, наступний результат поділіть на 13. А тепер цю частку поділіть на початкове двозначне число. Відкрийте книгу на сторінці, яка позначена одержаною часткою (в даному випадку на 37 сторінці). Я називаю перше слово на відкритій сторінці. Секрет фокусу пропоную вам розгадати самостійно, подумавши над ним удома».

Метою уроку-вистави є розширення знань учнів, умінь та навичок спілкування, співробітництва в процесі підготовки та виконання ролей; входження в образ (знайомство з біографією, характером, зовнішністю вченого, образ якого треба втілити) [4: 54].

Вистава, на відміну від рольової гри, передбачає більш чіткий сценарій, який регламентує діяльність учнів безпосередньо на уроці і збільшує їхню самостійність при підготовці сценарію. У виставі можна використовувати не лише теоретичний матеріал, задачі з теми, але й елементи історії математики, художню літературу, поезії, музику тощо. Однак важливо, щоб за зовнішньо привабливою формою уроку-вистави не втратити саму математику.

Наведемо фрагмент уроку-вистави «Побудова перерізів» (10 клас).

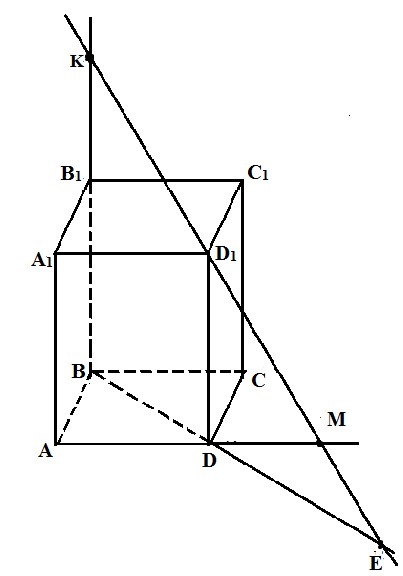
«Вчитель (роль виконує один з учнів):Французький математик Гаспар Монж, щоб спростити громіздкі обчислення для упорядкування планів військових споруд застосовував геометричні методи, розробивши в 60-70 роках XVIIIстоліття нову дисципліну – нарисну геометрію. Вона виявилась настільки важливою для оборони країни, що понад 20 років уряд Франції зберігав її як військову таємницю. І лише в 1799 році Монж видав перший підручник з нарисної геометрії, подавши в ньому методи для зображення на папері будь-яких тіл, які мають три виміри – довжину, ширину, висоту, за умови, що вони можуть бути точно задані. Дуже хотілося б, щоб і ви навчилися не лише вірно зображати просторові фігури на площині, але й розв’язувати задачі на побудову перерізів многогранників. Почнемо з найпростішої задачі: У прямокутному паралелепіпеді ABCDA₁B₁C₁D₁ на продовженні ребра ВВ₁ взято точку К, так, що В₁ лежить між точками В і К. Побудувати точку перетину прямої КD₁з площиною основи АВС.

Учень 1 (Роман). А що тут думати? У мене розвинута просторова уява!!! Я бачу цю точку!

Вчитель. Будь ласка, побудуй її.

Учень 1 (виконує побудову). Сполучимо точки К і D₁. Продовжимо КD₁ і АD. Очевидно, що вони перетнуться в точці М, яка і є шуканою.

Вчитель: Кажеш, що все очевидно?

Учень 1. Знаю, що ви хочете сказати: «Це не аксіома, а, отже, доведи». Доводжу! Точка М АD. АD АВС, то точка М належить площині АВС. Вірно? ТочкаМ КD₁? Отже,точка М – точка перетину прямої КD₁  з площиною основи паралелепіпеда, тобто і є шуканою точкою.

Вчитель. Але чи насправді точка М шукана?

Учень 2 (Антон). Ромо, невже таке може бути? В тебе пряма КD₁  перетинає площину АА₁D₁  у двох точках.

Учень 1. Як це в двох точках?

Учень 2. А так. Точка D₁  належить площині АА₁D_1.  Точка М АD, пряма АD належить площині АА₁D_1, то точка  М належить площині АА₁D₁.

Вчитель: Антон довів, що дві точки прямої КD₁ належать площині АА₁D₁. То що ж ми маємо далі?

Учениця 1 (продовжує). Тоді пряма КD₁ належить площині АА₁D₁, але ж точка К не належить цій площині. Отже, побудова виконана невірно.

Учень 1. (Задумавшись).  Але ж на рисунку все ...

Вчитель. Ромо, в задачі йде мова про прямокутний паралелепіпед. А наш рисунок – це зображення просторової фігури, а не сама фігура. Розумієш? Зображення її в паралельній проекції.

Учениця 2 (Таня). Ромо, а що можна сказати про прямі ВВ₁ і АD?

Учень 1. Вони мимобіжні.

Учениця 2. Вірно.Подивись уважно,прямі КD₁  і АD теж мимобіжні.

Учень 1. Тепер я вже бачу, що вони не перетинаються, бо пряма КD₁ перетинає грань АА₁D₁  в точці D₁, а пряма АD належить площині АА₁D₁ і не проходить через точку D₁.

Вчитель. А як же побудувати точку перетину прямої КD₁  з площиною АВС?

Учень 3 (Ілля): Я зрозумів у чому помилка Роми. В площині нижньої основи він вибрав пряму, яка мимобіжна з прямою КD₁, а треба було вибрати таку пряму, яка перетинається з прямою КD₁.

Вчитель. Вірно, Ілля. І яка ж це пряма?

Учень 3. Здається, я знаю.Прямі ВВ₁ і DD₁ паралельні, а, отже, лежать в одній площині. Тоді в цій площині лежать прямі ВD і КD₁. Отже, можна знайти їх точку перетину, тобто точку Е (виконує побудову).

Вчитель. Ілля правий. Друзі, запам’ятайте важливе твердження: щоб побудувати точку перетину прямої з даною площиною, потрібно в цій площині знайти пряму, що лежить в одній площині з даною прямою. Якщо дана і знайдена прямі перетинаються, то їх точка перетину – шукана.»

Кращі уроки-вистави студентів можна представити на конференції «Урок-вистава як засіб гуманізації та гуманітаризації навчання математики», участь в якій сприяє інтеграції знань (педагогіка, психологія, методика навчання математики тощо), підвищенню пізнавальної самостійності, дає усвідомлення того, що сучасна математика – складова загальносвітової культури і результат довгих і наполегливих пошуків багатьох поколінь.

Висновки. Під час проведення уроку-вистави з математики студенти мають можливість проявити не лише знання, але й творчість та отримати позитивні емоції. Російський радянський педагог  Ю. Бабанський наголошував: «Емоційний стан завжди пов’язаний із переживаннями, душевним хвилюванням: відгуком, співчуттям, радістю, гнівом, здивуванням. Саме тому до процесів уваги, запам’ятовування, осмислення в такому стані підключається глибоке внутрішнє переживання особистості, яке робить ці процеси інтенсивними, більш ефективними у досягненні цілей» [1].

Методи і прийоми для зацікавлення учнів математикою, з якими студенти знайомляться на заняттях з «Основ педагогічної майстерності», можна використати під час проходження педагогічної практики, мета якої «виробити у студентів уміння й навички, необхідні в майбутній педагогічній діяльності, закріпити теоретичні знання, застосувати їх у педагогічній практиці» [2: 268] .

БІБЛІОГРАФІЯ

1. Бабанский Ю. К. Методы обучения в современной общеобразовательной школе / Ю. К  Бабанский. – М.: Просвещение, 1985. –208 с.

2. Гончаренко С. Український педагогічний словник /С. Гончаренко. – К.:Либідь,1997.–376 с.

3. Воєвода А. Л. Елементи історії математики як засіб гуманізації навчання /А.  Л. Воєвода.  // Математика в рідній школі. – 2015. – № 4. – С. 31- 38.

4. Малафіїк І. В. Дидактика: навч. пос. [Електронний ресурс] – Режим доступу: www.uk.xlibx.com/.../22317-1-didaktika-reko...

5. Матяш О. І. Теоретичні та методичні засади формування методичної компетентності майбутнього вчителя математики до навчання учнів геометрії / О. І. Матяш. – Вінниця: ТОВ «Нілан-ЛТД», 2013. –  450 с.

6. Подласый И. П. Педагогика. 100 вопросов – 100 ответов: учеб. пос. для студентов вузов / И. П. Подласый. – М.:Изд-во Владос Пресс, 2006. – 365 с. 

7.Сисоєва С. О. Основи педагогічної творчості: підручник / С. О.Сисоєва – К.: Міленіум, 2006. – 244с.

8. Фридман Л. М. Психолого-педагогические основы обучения математике в школе /Л. М. Фридман. – М.: Просвещение, 1983. – 160 с.

ВІДОМОСТІ ПРО АВТОРА

Воєвода Аліна Ленідівна – кандидат педагогічних наук, доцент кафедри математики і методики навчання математики Вінницького державного педагогічного університету імені Михайла Коцюбинського.