ВИКОРИСТАННЯ ПРИНЦИПУ СИМЕТРІЇ ПРИ РОЗВ`ЯЗУВАННІ ЗАДАЧ З ФІЗИКИ У ВИЩИХ НАВЧАЛЬНИХ ЗАКЛАДАХ АВІАЦІЙНОГО ПРОФІЛЮ

Ольга Кузьменко
(Кіровоград, Україна)

У статті аналізується та розглядаєтьсяпоняття симетрії, яке покладено в основу сучасних фізичних теорій.Принципи симетрії використовуються в об’єднуючих фізичних теоріях. Проте слід відзначити, що теорія великого об’єднання, заснована на принципах симетрії, знаходиться у стадії розробки. Роль принципів інваріантності (у фізиці) ще не вичерпана, і ми далекі від універсального закону природи. Симетрія виявляє взаємозв´язок фізичних законів, спрощує розуміння складних процесів, що протікають у мікросвіті та розглядаються у фізиці.У статті простежено вплив принципу симетрії на розвиток умінь та навичок студентів при розв`язуванні задач у процесі навчання фізики, а також на їхню самостійну пізнавально-пошукову діяльність у вищих навчальних закладах авіаційного профілю. Розглянуто приклади розв`язування фізичних задач з розділу механіка.

Ключові слова: симетрія, навчальний процес, фізика, механіка, принципи симетрії, розв`язування задач.

В статье анализируется и рассматривается понятие симметрии, которое положено в основу современных физических теорий. Принципы симметрии используются в объединенных физических теориях. Однако следует отметить, что теория большого объединения, основанная на принципах симметрии, находится в стадии разработки. Роль принципов инвариантности (в физике) еще не исчерпана, и мы очень далеки от универсального закона природы. Симметрия обнаруживает взаемосвязь физических законов, упрощает понимание сложных процессов, которые протекают в микромире и рассматриваются в физике. В статье прослежено влияние принципа симметрии на развитие умений и навыков студентов при решении задач в процессе обучения физике, а также на их самостоятельную    познавательно-поисковую деятельность в высших учебных заведениях авиационного профиля. Рассмотрены примеры решения физических задач из раздела механика.

Ключевые слова: симметрия, учебный процесс, физика, механика, принципы симметрии, решение задач.

The concept of symmetry, which is fixed in basis of modern physical theories, is analysed and examined in the article. The principles of symmetry are used in unifying physical theories. However it should be noted that the theory of large association, based on the principles of symmetry, is in the stage of development. The role of principles of invariance (in physics) has not been outspent yet, and we are very far away from the universal natural law. Symmetry finds out connections of physical laws, simplifies understanding of difficult processes which are examined in physics. Influence of the principalof symmetry is traced on the development of abilities and skills of students in the process of tasks solutionwhile studying physics, and also on their independent cognitive searching activity in higher educational establishments of aviation type. The examples of solutions of physical tasks are considered from the section of mechanic.

Keywords: symmetry, educational process, physics, mechanics, principles of symmetry, solutions of tasks.

Постановка проблеми. Проблема розвитку та вдосконалення фізичної освіти є однією з центральних, яка перебуває в центрі уваги світового наукового та громадського співтовариства.Відповідно до актуальних завдань сучасної дидактики фізики, як педагогічної науки є пошук шляхів і засобів, які мають бути ефективними до практичного використання під час вивчення теоретичних досліджень та поєднання цих досліджень з практикою.

Загальний курс фізики, який вивчається студентами Кіровоградської льотної академії Національного авіаційного університету (КЛА НАУ) на першому курсі є базовим для підготовки операторів складних систем (ОСС) та є основою таких дисциплін: „Основи аеродинаміки та динаміки польоту”, „Основи радіоелектроніки та АСУ польотами”, „Теоретична механіка”, „Основи електротехніки та електрообладнання ПС та аеродромів” та ін. Під час вивчення курсу фізики студенти знайомляться з основними фундаментальними поняттями, законами, принципами фізики, явищами та експериментальними методами дослідження фізичних явищ і процесів природи, аналізом, синтезом, систематизацією спостережуваних явищ фізичного експерименту.

Слід відзначити, що одним із напрямків реформування фізичної освіти у вищих та в загальноосвітніх навчальних закладах є посилення її методологічної спрямованості. Тому виникає потреба, щоб фізика, як наука, сприймалась суб`єктом навчання не як перелік відкриттів чи наявність формул, а відповідно формувала наукове мислення у процесі пізнання навколишнього світу.

Рівень сформованості знань з фізики у студентів визначається засвоєнням фундаментальних фізичних понять, законів, теорії та принципів.

У сучасній фізиці виявлено певний взаємозв´язок фізичних законів і принципів симетрії. Особливо актуальні питання, пов´язані з теорією симетрії в сучасних фізичних теоріях, заснованих на об´єднанні фундаментальних взаємодій, тому що в сучасній теорії елементарних часток концепція симетрії відіграє важливу роль.

На нашу думку, варто сформувати у студентів під час вивчення загального курсу фізики цілісне уявлення про цю науку, відповідно на основі вивчення фундаментальних понять симетрії та принципів симетрії, а також використання цього поняття при розв`язуванні задач студентами у вищих навчальних закладах авіаційного профілю.

Аналіз останніх досліджень і публікацій. Основу методики навчання фізики у вищій школі досліджували в свої роботах О. І. Бугайов, С. У. Гончаренко, І. М. Кучерук, М. Т. Мартинюк, Л. І. Осадчук, Б. А. Сусь, М. І. Шут та ін.

Загальнонаукові категорії симетрії і асиметрії розглядалися в роботах B. С. Готта, Ф. М. Землянського, світоглядні питання в контексті теорії симетрії розглянуті Р. М. Ганієвим [2], проблемі симетрії у фізиці присвячені роботи Дж. Еліота, П. Добера [3], В. В. Мултановського, який розглядає симетрію у класичній механіці [5], І. З. Ковальова (розгляд симетрії в курсі фізики в середній школі) [4], геометричні перетворення симетрії розглядав М. М. Мурач [6], Е. Вігнер відзначав в своїх науковиз працях найважливіші проблеми філософського і природничо-наукового характеру, пов’язані з симетрією [1], М. І. Садовий розглядає в своїх роботах симетрію мікрочастинок [8].

Метою статті є аналіз та розгляд поняття симетрії, а також використання цього поняття при розв`язуванні задач з фізики студентами у вищих навчальних закладах авіаційного профілю.

Виклад основного матеріалу. Природа демонструє безліч симетричних об`єктів. Фактично ми маємо справу із симетрією скрізь, де спостерігається будь-яка впорядкованість.

Термін симетрія (σνµµετρνα) грецькою мовою означає «сумірність, пропорційність, однаковість у розміщенні частин» [6]. Симетричним називають об’єкт, який можна певним чином змінювати, дістаючи в результаті те, з чого почали.

Принцип симетрії, сформульований вперше французьким фізиком П`єром Кюрі, може широко використовуватися під час розв`язування задач з фізики у вищих навчальних закладах. Цей принцип полягає в наступному: 1) якщо причина має який-небудь елемент симетрії, то такий же елемент симетрії буде мати і наслідок; 2) деякі елементи симетрії наслідку не входять у сукупність елементів симетрії причин, тобто наслідок може містити додаткові елементи симетрії, які не містились в причині.

Під час розв’язування задач з механіки студентам слід використовувати такі елементи симетрії: площина симетрії, вісь симетрії, центр симетрії. Ці елементи симетрії знайомі студентам ще під час вивчення курсу геометрії, а також їх легко використати у процесі вивчення фізики у вищих навчальних закладах (ВНЗ). Слід звернути увагу студентів на те, що вони матимуть справу не з чисто геометричною симетрією, а з фізичною симетрією явищ та процесів, що вивчаються у фізиці.

Застосування принципу симетрії у процесі вивчення студентами загального курсу фізики у ВНЗ авіаційного профілю згідно з робочою програмою [7] вимагає виконання підготовчої роботи, яка полягає в наступному:

1. Знайомство з симетрією предметів і явищ у повсякденному житті. Потрібно мати на увазі, що в студентів першого курсу ці уявлення не чіткі, а також не зовсім послідовні, не досить осмисленні, тому в цей період викладач повинен уважно спрямувати діяльність студентів і виправляти їх уявлення про фізичні явища.
2. Використання поняття про симетрію фігур в курсі математики. Але слід зауважити, що в математиці геометрична симетрія вивчається досить глибоко, але застосовується недостатньо.
3. Поширення поняття симетрії геометричних фігур на фізичні об’єкти та явища.
4. Розгляд принципу симетрії.

Під час розв`язування задач з механіки доцільно скористатись принципом оборотності механічного руху, який можна розглядати як специфічну симетрію, що має місце при заміні знаку часу, тобто при перетворенні t→t. Закони механіки Ньютона мають важливу властивість: вони не змінюються при зміні знаку часу. Це означає, що коли тіло проходить певну послідовність станів відповідно до рівнянь механіки (розглядаючи ІІ закон Ньютона), то завжди можливий зворотний рух, при якому тіло буде проходити між стани, але в зворотній послідовності. Дійсно, при заміні t→-t величини, що входять в рівняння  перетворюються таким чином:

1. , тому що сила в основному залежить від віддалей між взаємодіючими тілами, що не змінюються при зміні знаку часу.
2. Згідно з означенням . Приt→-t маємо, що , а . Тому ; а значить .
3. Згідно з означенням маси, а також відповідно до характеру маси як фізичної величини маємо, що , тому що маса – це характеристика тіла.
4. Згідно з означенням прискорення . Але, тому що , то  при заміні знаку часу. Одночасно маємо, що при . Через це . Отже, . Таким чином, при заміні часу маємо: . Отже, якщо початкові умови одного руху співпадають з кінцевими умовами другого руху, то при зміні знаку часу тіло проходить ті ж стани, що і при прямому русі, але в зворотній послідовності. Це можливо лише при відсутності тертя.

Як приклад симетрії оборотності механічного руху, студентам слід розглянути рух тіла, кинутого вгору з певною початковою швидкістю з поверхні землі в однорідному полі тяжіння, коли не враховувати опір атмосфери.

Принцип симетрії можна застосовувати до розв`язання деяких задач з механіки, якщо разом з принципом оборотності врахувати і геометричні елементи симетрії.

Задача 1. Розглянемо рух матеріальної точки, кинутої під кутом до горизонту в однорідному полі тяжіння (рис.1).

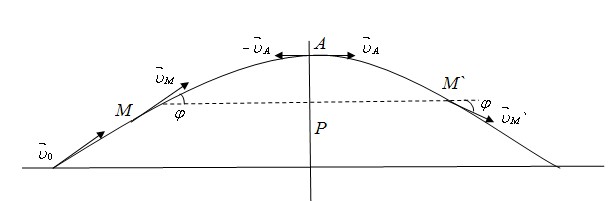
Рис.1

В цьому випадку, якщо не враховувати опір середовища, точка рухається по відрізку плоскої параболи. Ця парабола симетрична відносно площини Р. Рух матеріальної точки в будь-якому випадку визначається: діючими на неї силами, величиною і напрямом початкової швидкості точки, а також початковим положенням точки. В нашому випадку початкове положення точки визначається взаємним положенням в початковий момент рухомої точки і поверхні землі. Обираємо за початок відліку часу момент проходження точкою вершин траєкторії А. Коли до руху точки застосувати властивість оборотності механічного руху ( ), то одержимо , а величина і напрям сили тяжіння, і положення поверхні землі не змінюються. Отже, причини руху мають елементи симетрії: 1) площину симетрії, в якій лежить вектор , яка перпендикулярна до поверхні землі; 2) площина симетрії Р, яка проходить через точку А, перпендикулярно до  і до поверхні землі, причому з врахуванням оборотності механічного руху. Згідно з принципом симетрії, такі ж елементи симетрії має і наслідок – рух матеріальної точки, а саме: 1) симетрія руху відносна площини рис.1., тому траєкторія руху точки – плоска крива, що лежить в площині рисунку; 2) симетрія руху відносно відбивання в площині Р разом з відбивання часу; траєкторія симетрична відносно Р, а в будь-яких симетричних точках М і М` швидкості рівні по величині та складають однаковий кут з горизонтом.

Відомо, що рух центра ваги механічної системи визначається тільки зовнішніми силами; внутрішні сили положення центра ваги та його швидкість змінити не можуть. Тому, коли рухоме тіло розділяють на частини однакової маси, то ці частини будуть рухатись так, що в кожний момент часу кожна частина буде знаходитись на однаковій віддалі від центра ваги, тобто центр ваги буде весь час центром симетрії системи. Коли на систему діють зовнішні сили, що перпендикулярні до швидкості частинок в момент розривання, то в такому випадку центр ваги залишається центром симетрії одержаної системи.

Задача 2. Зенітний снаряд розривається на висоті h від землі на велике число осколків, що мають однакову початкову швидкість  і рівні маси. Знайти віддаль між двома осколками, що лежать на прямій, що проходить через центр ваги всієї системи і утворюють кут α з вертикаллю, через час  після розриву.

Розв`язок. У системі відліку, зв`язаної з центром ваги системи, яка рухається з прискоренням , осколки будуть розлітатись за всіма напрямками з швидкістю  кожен, а тому в момент часу  геометричним місцем точок, в яких знаходяться осколки, буде сфера радіуса , центр якої співпадає з центром ваги системи осколків.

Отже, в цьому випадку ми маємо симетричне розміщення осколків відносно центра ваги (центральна симетрія).Тому віддаль між двома осколками, що лежать на прямій, яка проходить через центр ваги системи, в момент  рівна діаметру сфери, тобто , і не залежить від кута α. Шукана віддаль рівна  до того моменту часу, коли осколок, що падає вертикально вниз, торкнеться поверхні землі і зупиниться.

Задача 3. У воді знаходиться кулька радіуса  і повітряна бульбашка такого ж радіусу. З якою силою взаємодіють кулька та бульбашка, коли віддаль між її центрами рівна . Як зміниться відповідь, коли стальну кульку замінити повітряною бульбашкою такого ж радіуса? Масою повітря в бульбашках знехтувати.

Принцип симетрії широко застосовують під час розв’язування задач на відшукування центру ваги різних тіл. Центром ваги тіла називається точка прикладання ваги даного тіла. Коли тіло однорідне та має центр симетрії, то центр ваги співпадає з центром симетрії. Це положення легко перевірити з допомогою принципу симетрії, при чому треба мати на увазі, що коли тіло сферично симетричне, то потрібно говорити не про однорідність тіла, а про сферичну симетрію в розподілі маси тіла. Коли тіло неоднорідне чи не має центру симетрії, то положення центру ваги обчислити важко, а то і зовсім неможливо. Центр ваги однорідних тіл і фігур, що мають центр симетрії співпадає з їх геометричними центрами.

Якщо пропонується в задачі відшукати центр ваги симетричної фігури, симетрія якої порушена (вирізано отвір чи до симетричної фігури прикріплена пластинка симетричної форми), то таку задачу студентам слід розв`язувати наступним чином: 1) виконують над тілом мисленнєву операцію, яка відновлює симетрію тіла, що була порушена, тобто вирізають симетричну порожнину, отвір, знімають прикріплені частини; 2) вважаючи ці додані чи відняті частини реально існуючими і враховуючи, що вони знаходяться там, де ми їх уявно розміщуємо за правилом моментів центр ваги заданої фігури як системи, що складається з двох симетричних тіл, центри ваги яких лежать в їх центрах симетрії. Потрібно вказати студентам на те, що в цьому випадку немає потреби користуватись поняттям від`ємної маси, застосування якої дає той же результат, але фізично нічим не виправдано.

Висновок. У результаті проведених досліджень констатуємо те, що доцільність підпорядкування змісту навчального матеріалу з фізики базується на фундаментальних поняттях, одним із яких є симетрія. Ознайомлення та вивчення студентами поняття симетрії та його принципів сприятиме формуванню сучасного наукового мислення, наукового світогляду, а також забезпечуватиме систематизацію знань з фізики при розв`язуванні задач з різних розділів фізики.

Перспективи подальших досліджень полягають в детальному аналізі поняття симетрії та його використанні у навчанні фізики у ВНЗ авіаційного профілю.

БІБЛІОГРАФІЯ

1. Вигнер Е. Этюды о симметрии / E. Вигнер. — М.: «МИР»,– 318с.
2. Ганиев Р.М. Групповая симметрия в множестве мировоззренческих высказываний / Роберт Маликович Ганиев. — Владикавказ: Северо-Осетинский гос. ун-т им. К.Л.Хетагурова, 2001. – 108 с.
3. Элиот Дж. Симметрия в физике / Дж. Элиот, П. Добер; Соч. в 2-х т. – М.:Мир, 1983. Т.1. – 1983. – 364 с.
4. Ковалев И.З. Учение о симметрии в курсе физики средней школы: автореф. дис. на соиск. учен. степени наук. канд. пед. наук : спец. 13.00.02 «Теория и методика обучения (физика)» / И.З. Ковалев. – К., 1976. – 24 с.
5. Мултановский В.В. Курс теоретической физики / Мултановский В.В. – М. : Просвещение, 1988. – 304 с.
6. Мурач М.М. Геометричні перетворення і симетрія / Мурач М. М. – К. : «Радянська школа», 1987. – 178 с.
7. Робоча програма з дисципліни «Фізика» для курсантів за напрямком підготовки 6.07102 «Аеронавігація», професійного спрямування «Обслуговування повітряного руху» / [укладач: В.В. Фоменко]. – Кіровоград: КЛА НАУ, 2013. – 22 с.
8. Садовий М.І. Окремі питання сучасної та традиційної фізики: навчальний посібник для студентів педагогічних навчальних закладів освіти / М. І. Садовий – Кіровоград: Видавництво ПП «Каліч О. Г.», 2007. – 138 с.

ВІДОМОСТІ ПРО АВТОРА

Кузьменко Ольга Степанівна – кандидат педагогічних наук, доцент кафедри фізико-математичних дисциплін Кіровоградської льотної академії Національного авіаційного університету.